JS1k 2019 writeup part 4 - Magical Light Tunnel

VIEW THE DEMO

My 2019 JS1k entry "Magical Light Tunnel" was inspired by Marks & Marks demo reel from circa 1981. I found that video years ago on YouTube and loved the old school audio and visuals. I decided to try and implement a section from it.

1. Copying and creativity

Most of the graphics in the demo reel are just wireframes and dots. They are visible even when they are behind other objects. This changes during the tunnel sequence - the lights that shouldn't be visible are clipped. I had done a short tunnel demo previously on dwitter.net and pavel did a remake of it that had clipping. I decided to use the same approach but using polygons instead of arcs. Soon I had the first version running.

I refined my new tunnel engine and got so inspired by it that suddenly I was filled with ideas. I wanted to let my creativity out instead of carbon copying the video. I collected more inspiration by searching light tunnel videos and hallway architecture images. Below are some notes I had written down.

• Create shapeshifter plugins that alter the tunnel shape
• Create switcher plugins that turn individual lights on / off
• The further you go, the more you experience
• Let's create something special!

Going from copying to creating is something that happens often with arts. Don't wait for inspiration - start to work and you will find it!

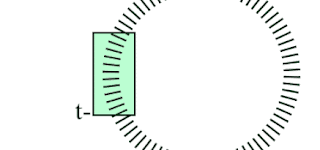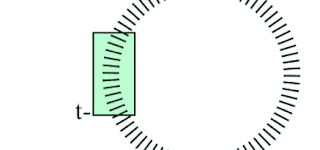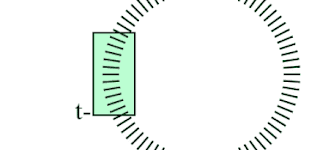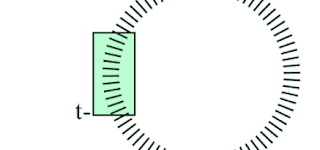
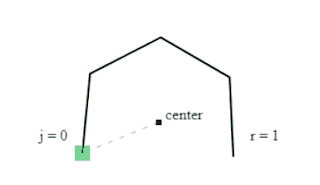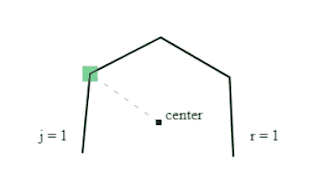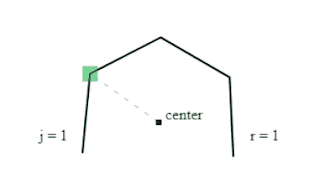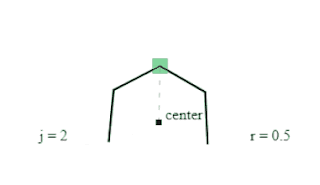
2 . Tunnel engine

The tunnel engine is best described by a set of requirements and illustrations...

• Tunnel is a loop of indexed layers
• Viewer position in the tunnel is t
• Visible segment is 24 layers forward from t

• Layers are closed 2D polygons that have 24 sides
• Polygons are drawn front to back
• Each polygon forms a clipping area that clips the drawing of the next layer
• Polygons are filled with transparent color
• Polygon sides are sometimes drawn to form a gate
• Polygons are scaled based on distance from viewer

 

• Polygon points are lights that are either on or off
• Polygon has a center that is the local space origin for its points
• Polygon points are vectors created with rotation formula
• Vectors can have varying length

 

The importance of clipping is easy to understand from the comparison below. On the left the polygon outlines are drawn for each layer in full. Clipping makes the tunnel more realistic and clean looking.

3. Shapeshifters

Shapeshifter plugins manipulate vector length based on position of layer and current point index j. They return a multiplier to use in rotation formula calculation. Below you can see how the shapeshifter formulas alter the tunnel shape. First shape is the default where each polygon point vector has a length of 1. It can be mixed with the square shape to form a cool corridor. Square can also be tilted to form a spiral tunnel. The third shape I call the circus entrance. Last example is a cave achieved with filter expression Math.sin(j >> 1 & p) / 3 + 1 where j is index of current polygon point and p is layer position. Because p is different for each layer we get variations in the resulting shape.

4. Switchers

Switchers decide if the current polygon point light source is switched on or off. They are expressions that resolve to true or false based on input and are used to animate the lights. At the very beginning of the demo we only activate two lights on opposite sides to create railings. The expression for this is j % 17 == 3. When we only want the top lights on we can use j > 9 & j < 14 which we can shorten to j % 14 > 9.

To get more complicated patterns we'll use more arguments. For example Math.sin(j + p + t) < 0 gives us a hypnotic spiral.

I created a lot of different filters and chose the ones that had the best bang for the buck. These filters were then arranged to form a storyline where things would get more interesting the further we go. I ended up with a really long demo. I got comments that maybe it was a bit too long so I got rid of some of the filters to make room for a surprise ending...

5. Breakout

So there needs to be a treasure behind the crystal cave. 3D diamond was my first thought but it was too obvious. I wanted something that the viewer wouldn't expect but at the same time it would make sense in a programming competition. I had done mini tribute demos of Tetris, Breakout, Defender and Invader and I knew I could do any of them with the remaining bytes. Breakout was the most suitable choice. It has walls just like the tunnel and I could do physics that react with them. Below is a short screen capture from dwitter.net.

6. Conclusion and source code

I really hope JS1k 2019 won't be the last time this awesome competition is arranged. It has inspired and entertained programmers worldwide. It was my introduction to code golfing in 2013 and what a journey it has been. Huge thanks to the organizer Peter van der Zee and all the participants and judges throughout the years!

At the bottom is the commented source code. I hope you enjoyed the demo and this article.

Follow me on Twitter if you want to hear of new demos and blog updates - @jylikangas

JS1k 2019 writeup part 3 - Strigiformes

VIEW THE DEMO

Most of my better known wildlife images are of owls and birds of prey have fascinated me since I was a little boy. Once while going through images on Pinterest I saw a cool art design where feathers had owl heads. It was created by Oleksandra Barysheva and can be seen on her Threadless page. I decided to try and do my version of it and see how many recognizable owls I could fit in 1024 bytes of JavaScript...

1. Feather function

To draw one side of the feather we first build two nested loops. Inner loop draws a single barb away from the shaft while the outer loop moves us upwards to the next starting position.

for(j=120;j--;)for(i=j;i--;c.fillRect(i,-j-i,1,1));

The above code shows the basic loop structure. Then step by step we begin to add rules for the barb length and make them curve resulting in a very natural looking shape...

We then put this loop inside a function which allows us to use arguments for variation. To create the other side of the feather we can use scale(-1,1) to flip the x-axis and then call our function again.

Now that we are happy with the shape of the feather we can add colors. We make the brightness change based on the values of loop iterators. The shaft and first barbs need to be white. A nice gradient for the length of the barb and some natural looking variation and our feather function is complete.

2. Drawing the head in layers

To start the owl's head we use arc to draw an unfinished circle. On top of that we draw darker colored rays shooting out from the center. The tricky part is creating a loop to draw the two discs that are characteristic of owls. Eyes are in the center of these discs. Color of pixels change as we go further away from the center. Texture is achieved by adding smaller scale contrast changes using remainder. Eyebrows are done in similar fashion on top of the disc. Last but not least we do the peak with two small rects...

3. Repeating code

One of the strategies to fit a lot of code into 1kb is making different parts of the code look the same. The packer can heavily compress these repetitions. After I had done the great grey owl I repeated the same code and made just enough changes so that the next owl would be recognizable. I kept doing more species until I was out of space. To finalize the demo I grouped the owls nicely instead of having them in a line. I also came up with a variation to the feathers so it would look like some of the owls are spreading their wings.

Follow me on Twitter if you want to hear of new demos and blog updates - @jylikangas

JS1k 2019 writeup part 2 - ShadowBoX

VIEW THE DEMO

Shadow box is a display case where objects are placed in layers to achieve depth effect. It was originally used to present memorabilia, but artists have taken this concept much further to create little worlds inside the frames. The most typical approach seems to be to cut silhouettes from cardboard and put led lights behind them. End results can be stunning. Creating a nature landscape in this style was the initial idea behind my ShadowBoX demo. As often happens once you start to work on something it can take a life of its own...

1. Recycling

To get off to a quick start I reused some of my dwitter.net codes. To build the trees I used a recursive function lifted from my "Fractal In The Wind" demo. I tried to avoid the typical straight lines look so I drew the trunk and branches with curves and set lineCap to round. I made the trees bend towards the center so they create a more intimate feel. Hills I could pretty much directly copy from "Parallax Mountains". I mixed the two together and added a CSS radial-gradient background. Just like that I had a PoC version done...

To give the landscape a more organic feel I added some randomly placed plants. They filled up the ground nicely and I though I could spend rest of the bytes on the storyline and animated objects. Since it was a moonlit scene having an owl flying towards the viewer was a must. I stumbled across a goofy bat animation on the internet and tried implementing something similar. I used the same drawing approach for the owl as I did for the car in the "Cruising the 80s" demo. Sine waves always provide a simple way to achieve natural looking movement. Adding rotation made the owl more interesting and unpredictable.

2. Simple solutions

At this point I thought I had a nice demo and could just polish it. Once I showed it to a colleague of mine, Rami Repola, he immediately commented that it should have fog and lightning. My initial reaction was of course "try to add that with one hundred bytes yourself!" Soon I realized that such effects would work really well to form a storyline. Only problem was that they'd require lots of new code. Or would they?

I realized that I already have trees which are kind of like lightning when you think about it. So I did a very simple variation of the recursive tree function. Also I could just bypass setting the background color of the canvas element during the lightning strikes and it would be left at the default white color. Best solutions often seem obvious but somehow are really hard to spot at first.

Because I'm using CSS to set the background color, the actual canvas is kept transparent. I draw some white pixels on the top of the screen. They have anti-aliasing, so when I make a huge stretched copy of them with drawImage, they are just this big blurred area. When I saw how well it worked I was really happy with myself for a moment. :)

3. Snowstorm

Doing weather effects reminded me that I also had a very short snowstorm implementation in "Magical Winter Forest" dweet.

Well why not add that to the mix as well!

4. Golfing never ends

If there is one thing I've learned about code golfing it is that there always seem to be more ways to make things simpler and shorter. When something motivates you to try harder you will eventually find a way. Although I had already spent the allowed kilobyte, I started to have more ideas for the demo. It could be great if the scene was beautiful and peaceful at first before things get crazy. Something like a sunrise and swans in the lake. Back to work!

I needed to change the composition and adjust the background color. I made the trees move when the storm comes. And wouldn't it be great if that owl attacked the viewer in the end!

One thing I eventually had to leave out was the framing of the box. No biggie really. Last little adjustment was to drop the frame rate lower for an old cartoon animation feel. I really love this demo and I'm planning to program more shadow boxes later just for fun!

Follow me on Twitter if you want to hear of new demos and blog updates - @jylikangas

JS1k 2019 writeup part 1 - Cruising The 80s

VIEW THE DEMO

When I did a blog post about my "Cyber Auroras" demo a year ago the conclusion I wrote was this:

Inspiration and personal connection to the subjects will drive you to better performance and leave you a much happier programmer!

I had forgotten about writing that but luckily I had not forgotten the lesson learned. What that mentality has allowed me to achieve in the past year as a programmer is nothing short of amazing on a personal level. I went on to write countless 140 byte dwitter.net demos learning more about code golfing than in my previous years combined. It also made me go back to the fundamentals of JavaScript programming and I filled some important gaps in my understanding of them. This made me a better software developer in all areas - not just in code golfing.

When the 10th (and hopefully not final) JS1k came along I had many ideas and tricks to choose from. This resulted in the release of four very different demos which I'll now introduce to you one by one...

1. Retrowave

I went through a period last winter where I was really into the retrowave visuals and atmosphere. I spent one weekend trying to find the smallest possible snippets of code for producing each of the synthwave art cliche elements. I had a lot of fun combining some of them into dwitter demos.

When JS1k 2019 started I went back to that bag of tricks first and put the grid and the sunset as the backdrop for the demo. I wanted to add palm trees and a Lamborghini Countach to go all out on the theme...

2. Compressing SVG paths

I had previously experimented with Path2D drawing and finding ways to heavily compress the data. The approach I chose is based on the ability to scale and mirror the paths. The shape needs to be symmetrical and simple enough to draw half of it with a 10 x 10 grid. We will then need only one byte for each coordinate and only half of the coordinates need to be defined. I drew both the palm tree and the car with an online SVG Path Builder and compressed the data by hand.

Here's the code that draws the chassis of the Lamborghini with the coordinate range of 0-9 for both axes...

c.fill(P=new Path2D('M'+[...'944000014163040989']))

c.scale(-1,1);c.fill(P)

And here's how the path looks...

The data is a string of coordinates. M is the moveto command, but it turns into lineto automatically if you add more coordinates after the initial position. I've crammed all numbers together to save space and I use the spread operator to separate them. This goes as input for the array literal syntax that creates an array that has our coordinates as elements. When we add this array to the string "M" it is converted back to a string by the JS engine.  Below is this process step by step from the Chrome console so you can see what the interpreter does with our data...

Since we use fill it will close the path automatically for us. We don't need to define the last coordinate of the path.

For some special cases this approach could be taken even further by using relative coordinates and packing them inside 3-4 bits each. But that's for another demo in the future. :)

3. Adding details

To make the car look more authentic I added details around the chassis. The mirrors and the spoiler are done with simple rects drawn before the chassis and in slightly different shade of grey. This adds depth. The windscreen reuses a section of the chassis path and is slightly transparent. To mask the blockiness of the design I used a linear gradient to paint the car. It cost a lot of bytes but also makes a big difference. The glowing lights are a stack of scaled transparent white rects with shadowBlur.

4. Making music

You can't have a synthwave demo without music, right? As a longtime guitarist and songwriter I was very excited to start working on audio.  I had never done anything with the audio context in the past and sadly my initial excitement was soon gone after realizing the limitations of it. Not only does setting it all up take a lot of space but the basic sounds are just plain awful. I had to drop my dreams of a good sounding track and try to create something that was bad but hopefully bad in a good way.

The song itself I had composed years ago for the unfinished game called Owl Invasion. It was just one track of fingerstyle acoustic guitar produced into an electronic song. I split the bassline and melody to different oscillators and broke down the song into a code logic rather than trying to compress the data. I eventually managed to fit the parts in surprisingly small space but it really is just a complex set of brute force code golfing without a clear idea behind it. It worked but it's not pretty nor easily explainable.

I initially connected two oscillators to the same destination. After posting the demo I was informed that in some environments the sounds were painful to listen to. I replaced my first version with one that uses two destinations and also used less distorting oscillators. Luckily I managed to fit the changes without making any sacrifices in the visuals. I really like how during the chorus the background is animated to change into a desert scene.

Follow me on Twitter if you want to hear of new demos and blog updates - @jylikangas

Making of Wireframe World

VIEW THE DEMO

For some time I've been trying to come up with a way to do a 3D wireframe landscape within the 140 byte size limit of Dwitter. This article details how I finally managed to pull it off.

1. The grid

Wireframe landscape is very tricky to do in limited space. The reason is the need to use the HTML5 Canvas API path drawing methods. The calls to x.beginPath(), x.lineTo() and x.stroke() already take up 33 bytes and that's not counting the statement separation. Also you need to call lineTo at least twice with different arguments to actually draw a line segment so you have to be really creative with the way you arrange the code. As usual lets start in 2D to keep things simple. Wireframe landscape can be thought of as a perfectly symmetrical grid but with height information stored for each vertex. So looking directly from above, it looks like a regular grid...

I know this might look boring unless you are really into Xs and Os. To draw a square we need four lines. With a grid we can cheat and just do two for each square...

With this simplification we've saved two calls to lineTo but our grid has two ugly unfinished edges. This is not a problem as we will make sure those are never visible in the demo.

So we are drawing only the left and top edges and the neighbors will take care of the rest. To do this efficiently the best solution I could come up with is to start from bottom left corner and then move to top left and top right corners. I've made a very important illustration to show this...

First we need to move to the right position. Normally this would be done with moveTo-method but lineTo works the same way when there is no previous points in the path. The movement sequence could be written X1,Y2 -> X1,Y1 -> X2,Y1. I'll just show you the full source code and then we'll break it into parts...

for(c.width=i=-9;++i<9;R=a=>x.lineTo(150+a*99/(z=j-t%1),z+90+(99+T(j+t&a+9|8)+a*a)/z))for(j=12;x.beginPath(x.stroke()),R(i),--j;R(i+1))R(i)

The grid points are done as expected with two nested loops. Outer loop with the variable i defines the x-coordinates and j defines the y-coordinates. The horizontal loop is centered around zero for simpler perspective projection and goes from left to right. The vertical loop goes backwards from 11 to 1. It's important to stop at one to avoid getting negative values for our perspective divider z. We create a function R that encapsulates the projection and path drawing. Arrow function syntax is naturally very suitable for code golfing. We'll use an argument a to pass an x-coordinate to the function and we can use j directly from global scope. Now we have our loops ready and a function that draws lines for us. Next we'll take a deeper look into the magic of the for-loop.

2. Understanding the for-loop

It is really important for any programmer to fully understand how a for-loop works. It is not necessarily obvious in which order statements and code are run so here is a quick reminder.

for(A;B;D){C}

• Statement A is executed first and only once before the looping starts. It is used to initialize the loop
• Statement B is executed before each repetition of the loop. It is the condition for running the loop. If it evaluates to false the loop stops, otherwise the loop will continue running
• Code block C is executed if condition B was met
• Statement D is executed after each repetition of code block C. Loop variable is often incremented here, but that is optional

Our inner loop looks like this. Lets go through what happens

for(j=12;x.beginPath(x.stroke()),R(i),--j;R(i+1))R(i)

In initialization we declare a variable j and set it to 12. For our conditional statement we are grouping statements in a way that some functions are called before the actual condition. This is something that is not normally done but allows us to run code before we change the value of j. The first function we call is x.stroke() which draws the current path. Since there is no path at first nothing is drawn, but we save one byte by placing it here as a useless argument. Then x.beginPath() gets called and starts a new path for us. Then we move to "X1,Y2" by doing our first call to R(). We pass our current x-coordinate i as an argument and the function uses our y-coordinate j directly. Then we decrement j and call R() again to draw our first segment to "X1,Y1". Notice here that the loop is now running the code block after evaluating the condition. Once --j evaluates to zero, the loop is stopped. Because we decrement first and then evaluate the condition, our code block will not run when j is zero. Noticing this optimization trick saved me 2 bytes and allowed me to fit the demo in 140 bytes after being stuck at 141 for several days. So why is this imporant. Well if we went to zero, we'd need to add 1 to our z calculation like this z=j-t%1+1. After this the last statement is executed. Now we need to draw a line to "X2,Y1" so we pass i+1 as the argument. Now our path is complete and during the next repetition it gets drawn to canvas by a call to x.stroke().

The lesson here is that there are many ways you can use the for-loop. We are so used to sticking to the most common structures that it can be hard to notice when we benefit from a different approach.

3. Going 3D

Lets assume our grid lies flat on the floor. From where we look at it the horizontal axis is X and vertical axis is Y. Since it's flat, Y is constant. Lets have an axis perpendicular to X on the same plane and call it Z. This can approximately be thought of as our distance from any of the grid points. To achieve perspective projection we just need to divide both X and Y by Z. In our demo we could do it like this...

R=a=>x.lineTo(150+a*40/(z=j),90+90/z) 

Now we could use some movement. We want to go forward which means our distance should decrease. We do this by subtracting time from z. Our grid is limited in size so we will do a loop by using modulus operator...

R=a=>x.lineTo(150+a*40/((z=j-t%1)),90+90/z)

At this point my small 3D wireframe engine is working, but it's not very interesting. I tried to do various random terrains but wasn't happy with them. Then I remembered a cool unfinished JS1K demo by Bálint Csala and decided to do a small planet that spins around and has little spiky mountains. I like spruce trees so the end results also reminds me of Taiga landscapes. Anyway to make it seem like we are on a small planet we need to make the grid round both horizontally and vertically. Here's how I did it...

R=a=>x.lineTo(150+a*80/((z=j-t%1)),z+90+90/z+a*a/z)

This also effectively hides the ugly right edge of our grid. Now all we need is those spikes. It really is not easy to add any type of recognicable architecture to a 3D model this small. Often the best solution is to use trigonometric functions. This time I experimented with tangent planes until I found something I liked...

R=a=>x.lineTo(150+a*80/((z=j-t%1)),z+90+90/z+a*a/z+T(j+t&a+9|8)/z)

A bit more code golfing trickery and that's all of Wireframe World. I just wish there was room to use some 80s colors on black background.

Follow me on Twitter if you want to hear of new demos and blog updates - @jylikangas

Making of Neon City Wakes Up

VIEW THE DEMO

I love retro pixel art and 80s graphics in general. I also like to program in an old school way with bitwise operations and all that glam rock. I'm just telling this so you all would understand why this demo is so incredibly last season. Here we go again on our own...

1. Pixel array approach

When I do raycasting I often manipulate the Canvas ImageData array directly. For Dwitter demos that approach is not feasible because the calls to getImageData and putImageData take a lot of space. There is a way to simulate it though. We can use fillRect to draw each pixel on the screen separately and then control them either by setting color with fillStyle or by simply switching pixel width between 1 and 0 and doing black and white. This changes the way we look at drawing on screen as we are drawing every pixel by default and the logic will either define what not to draw or at what color. For the sake of simplicity, lets first look at the case of each pixel on screen being either drawn or not drawn and build our city skyline this way. We have the Dwitter boilerplate and all we need in addition is a tight loop that draws the screen full of small rects...

for(c.width=i=110;i--;)for(j=64;j--;)x.fillRect(i,j,1,1)

That should paint our whole screen black. Basically i is our screen x and j is screen y. If you change the width in fillRect to 0, the screen is left white. 0.5 will make it grey. Adding a conditional statement there lets us control the image. Just to show how it works here's how you'd do a flat horizon...

x.fillRect(i,j,j>32,1)

So if our current screen y coordinate is larger than 32 the width of the rect will be 1, otherwise 0. This results in only the lower half of the screen being black. Now lets get busy and do the silhouette of the buildings using this method...

2. Adding conditions

x.fillRect(i,j,j/9>3+S(i|3),1)

I'm quite proud of this little formula that gives us the city in 12 bytes. It's easier to read as  j>27+S(i|3)*9 but we save an extra byte by scaling things down. The condition basically tells the browser to only draw when the current pixel is below our little sine wave. The blockiness is achieved with the bitwise OR operation. Now to something much more complex - adding the reflections on water...

x.fillRect(i,j,j/8<6+C(i-j-t)&j/9>3+S(i|3),1)

The idea is the same but we don't need the OR operation and we make the reflections angled by adding j to the mix. Well actually subtracting it but you get the idea. Variable t is elapsed time and gives us movement. We use the AND operator to make sure both conditions are met before we draw pixels. Seems to be working nicely and only 82 bytes spent in total. Time for details!

Many 80s computer graphics had wireframe grids vanishing to the horizon and a sun that had horizontal lines going over it. We will simplify this by just doing horizontal lines on the sky - again by adding a condition...

x.fillRect(i,j,j/8<6+C(i-j-t)&(j/9>3+S(i|3)|j%7<1),1)

Only 8 more bytes thanks to the modulus operator! We don't want the lines on water so we need to combine our new condition with our building condition. This requires adding parenthesis. We use the bitwise OR to draw if either condition is true. Notice what a big difference these horizontal lines make in making the image recognizable. Up next, the stars...

x.fillRect(i,j,j/8<6+C(i-j-t)&(j/9>3+S(i|3)|j%7<1)|!(1+j*i&79),1)

12 bytes for a starry sky that reflects on the ocean isn't all that bad. We multiply our x and y coordinates and use some bitwise magic to scatter the stars all over the screen. The logical NOT operator turns the result of our formula into 1 if it's anything other than 0. You might wonder why we add one in the beginning - that's so we don't get a vertical black line on our left edge when we are multiplying zero with zero. Now we have added 4 layers of fairly short conditions. With these rules the end results is a 102 byte black and white version of the demo. I used the remaining space to add animated neon colors and higher resolution. I also changed the order of conditions slightly to separate layers into 3 groups of base color.

3. Code golfing tip

To finish I'll point out one code golfing trick that helped me fit this demo inside the Dwitter limit of 140 byte...

x.fillRect(i*T,j*T,T=18,T)

To get larger pixels for the high resolution version I needed to multiply each argument by 18. The first time I need it is not the best place to define a variable cause I'd have to use parenthesis. What we can do is use a variable that has already been declared in the boilerplate. We don't need Math.tan in our demo so I chose the provided shorthand T. When fillRect is first called it doesn't draw anything cause T is not a number. The second time and from then on the value of T is 18.

I hope you enjoyed this article. Would love to see your work on Dwitter too!

Follow me on Twitter if you want to hear of new demos and blog updates - @jylikangas

Making of White Room Traps You

VIEW THE DEMO

This time we'll try to create a 3D wireframe cube with the smallest possible charcount. I think that you should always put extra effort into simplifying the object or rendering technique that is the center of your demo. If we can manage to do the cube with circa 100 bytes that leaves us plenty of (white) room to build something special. In the case of my Dwitter demo "White Room Traps You" the box gets some nice shading and becomes alive to trap you inside. Spooky.

1. Start with 2D

Before trying anything in 3D it can help to do a 2D version first. Cube in two dimensions is a square. Since it's perfectly symmetrical we can define it as the largest square that fits inside a circle of a given radius. So we only need a radius - no vertices! We have four corners so we go around a circle in steps of 90 degrees and draw lines between those points like in the animation below...

When we have a flat object parallel to the x-axis we can imagine creating another copy with different y-axis position. When we connect the corners we end up with a 3D wireframe version...

Now we have visualized in a simple way what a cube essentially is. Next we'll look at an efficient way to render it in a single loop.

2. Rendering the cube with a single loop

I often approach a problem with pen and paper before programming anything. To solve this puzzle I drew a 3D cube and followed the edges with a pen to find a simple way to visit all the edges. Since I'm a programmer I can automatically think of the required logic for different paths. It seemed the easiest way was to draw a square wave going around the cube once and then another but with inverted phase. Let's first draw a square wave...

Then do it in 3D around a center point...

Then do the same inverted...

Cube is what happens when we put the two together. But instead of inverting the phase and doing another round we can start to go backwards when we meet our own tail. This keeps the pattern of consecutive vertical and horizontal movements going thus making our JavaScript implementation smaller.

Of course we are drawing some edges twice but dirty tricks are what code golfing is all about. Plus it adds character to the box. Lets look at some code already!

That's the smallest and ugliest rotating wireframe box I could do with the Dwitter boilerplate. I'll try to explain what's going on in the 87 bytes. First we define our canvas size which also will clean it. We will use 64 for the loop repetition count even though 16 would be enough. Again it doesn't matter that we are drawing edges multiple times and we save space when we don't need to define another number. There's also no need to use functions like moveTo, beginPath or closePath usually associated with path drawing. We just keep calling lineTo without worrying about performance or super clean lines. Here's what's going on with our line drawing coordinates if we clean it up...

X = 32 + S(t += (7 - i) % 2 * 1.57) * 20

The first number, 32, is just an offset that places us nicely on the center of the canvas. The radius of the bounding circle is 20 and for x-coordinate we need to multiply that with the sine of our current angle. The angle t is incremented every other round in steps of 1.57 (approximation of PI / 2) with the help of the modulus operator. Manipulating the variable t as our angle is a nice code golfing trick because it's predefined by the framework and resets to elapsed time before each call to u. It gives us rotation animation with only 1 extra byte versus a static cube. A byte well spent I'd say. However the most important part to note is that we turn backwards after 8 iterations by using 7 - i.

Y = 9 + (i % 4 >> 1) * 20 + C(t) * 5

For y-coordinate we multiply the radius by 0 or 1 based on if we are drawing the top or bottom edges of the cube. We need to alternate every other round which is a bit more tricky. The more typical case, which we already had with the angle change, would be to alternate each time by using i % 2. We need to manipulate this by taking the remainder of i divided by 4, then diving it by 2 and rounding down. In the last part we add the cosine of current angle multiplied by 5 to get nice parallel projection.

That's a lot of text and images to explain 87 bytes but we did it! I feel this was the most important part of the demo. Without getting the cube down to this size it would be impossible to add exciting visual additions and a storyline which we'll discuss next.

3. Fake shading

Having a lot of space left allows us to use more of the Canvas API possibilities. I'd seen other Dweets use drawImage function for cool effects and wanted to try some things with it myself. The function can be used to create a copy of the current canvas or a part of it and draw it in another position. This can be useful for a mirror effect by combining it with scale or rotate function. What I did here was to adjust globalAlpha to 0.1 and copy the canvas onto itself at each iteration but with incrementing y-position. Since the stroke-function is drawing the lines several times at the same position they look dense. But the copies are moved so they remain transparent.

drawImage(c,globalAlpha=.1,i)

Below you can see the difference this subtle shading trick makes. I think it adds a sense of atmosphere and presence to a simple wireframe object...

At this point I was very excited how the demo was evolving and knew I had to fit a storyline to it.

4. Animating with perspective projection manipulation

When you want to manipulate how an object looks you have two options. Either you actually change the shape of the object by adjusting the data or you just change the way it is rendered. For our cube we could change the radius over time to make it larger. While this would otherwise work for the demo it would require more bytes than adjusting the projection variables. What we will do is change our perspective divider Z when the combination of elapsed time and current angle gets past 6.

Z=(t<6)+1+C(t)

What this does is zoom us inside the box over time. Because we do this to one corner at a time the sides of the box appear to open and wrap around us. I hope people actually let the demo run long enough to notice this. :) So that's my white room (without black curtains) which I personally think is among my nicest dweets. I leave you with the full 140 byte source code. Follow me on Twitter if you want to hear of new demos and blog updates - @jylikangas

with(x)for(i=16,c.width=198;i--;stroke()&drawImage(c,globalAlpha=.1,i))

lineTo(99+S(t+=(7-i)%2/.64)*99/(Z=(t<6)+1+C(t)),49+((i%4/2<<6)-25)/Z)